(1)

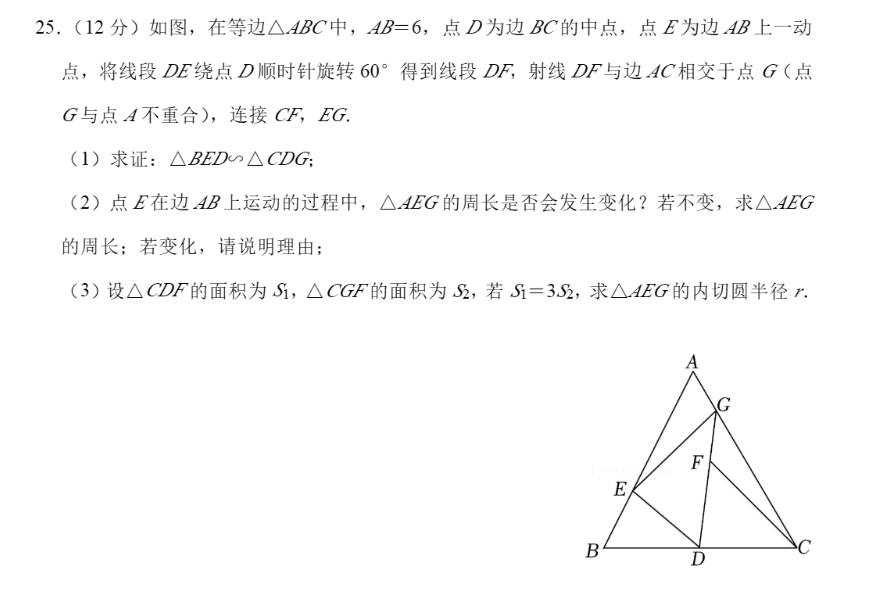
第一问还是比较简单的，所以简写一下。

$\because \angle EDG=60^\circ \\ \therefore \angle EDB+\angle BED= \angle EDB+\angle CDG=120 ^\circ \\ \therefore \angle BED=\angle CDG \\ \therefore \bigtriangleup BED \sim \bigtriangleup CDG \\$

(2)

过程有点多，写个大纲差不多了。

这题让我们判断 $C_{\bigtriangleup AEG}$ 是否为定值，我们可以先盲猜它是定值（毕竟一般这种题都是定值）。然后观察 $\bigtriangleup AEG$ 所在的位置，发现其中 $EG$ 和 $AG$ 的位置比较刁钻，不好求，于是我们可以想到过点 $E$ 作 $AC$ 的垂线，如图所示：

这样是不是就把 $EG$ 和 $AG$ 跟 $EH$ 联系起来了（$AG=AH-GH$），同时，$AE$ 和 $AH$、$EH$ 也联系起来了。但是，我们是不知道它们的具体数值的，于是我们直接设元：设 $BE=a，AE=6-a$。这里我们需要注意到，为了求 $AG$ 关于 $a$ 的表达式，我们需要 $CG$，而 $CG$ 需要用第一问的相似得到，所以我们设 $BE$ 为基本单位。

有了上面的准备之后，剩下的直接爆算。

$\because \bigtriangleup BED \sim \bigtriangleup CDG \\ \therefore \frac{BD}{CG}=\frac{BE}{CD} \Rightarrow \frac{3}{CG}=\frac{a}{3} \Rightarrow CG=\frac{9}{a} \\ \therefore AG=AC-CG=6-\frac{9}{a}$

至此，$\bigtriangleup AEG$ 中的 $AE$ 和 $AG$ 都用 $a$ 表达出来了，只剩下 $EG$ 了。那么如何求 $EG$ 呢？这是很好办的，$\angle AHE=90^\circ，AE=a$，因此可以用三角函数求出 $AH$ 和 $EH$ 关于 $a$ 的表达式。

$EH=AE \times \sin A=3 \sqrt{3} - \frac{\sqrt{3}}{2}a \\ AH=AE \times \cos A=\frac{1}{2} \times (6-a)=3-\frac{a}{2} \\ GH=GC-CH=(AC-AG)-(AC-AH)=AC-AG-AC+AH=AH-AG=3-\frac{a}{2} - 6-\frac{9}{a}=\frac{9}{a}-3-\frac{a}{2}$

然后在 $\bigtriangleup EGH$ 中使用勾股定理：

$EG=\sqrt{GH^2+EH^2}=a-3+\frac{9}{a}$

至此，$\bigtriangleup AEG$ 的三边都用 $a$ 表示出来了，所以直接求周长就好啦。

$\therefore C_{\bigtriangleup AEG}=9$

(3)

有了前面两问，第三问不是易如反掌？

首先，三角形的内切圆圆心是它的三个角平分线的交点，它到三边的距离相等。其实不知道也可以

所以我们直接拿内切圆半径公式求就行了，$r=\frac{2\times S}{C}$。这个柿子很好推我就不推了。

第二问中，我们求出了 $C_{\bigtriangleup EGH}$，差个面积。而要求面积，就要 $AG$ 和 $EH$，这两个玩意我们都已经用 $a$ 表示出来了，所以求 $a$ 就行了。那么怎么求 $a$ 呢？可以发现第三中它给了一个 $S_{1}=3 S_{2}$，因为这两个三角形高是相等的，所以它们的面积之比就等于底边之比，即 $\frac{DF}{GF}=\frac{3}{1}$，故有 $DF=\frac{3}{4}DG$，易证 $\bigtriangleup DEF$ 是等边三角形，故 $DF=DE$，即 $DF=\frac{3}{4}DG$，然后用第一问的相似和第二问中设的元列出一个关于 $a$ 的方程，解出 $a$，代入计算即可。

最后答案为 $\frac{5\sqrt{3}}{12}$